量化专题：股指期货套期保值方法分析lg...

　　来源：国投安信期货

　　在股指期货套期保值的过程中，基差择时和对冲比率一直是普遍关注的核心问题。从近年情况来看，股指期货在经历了深度贴水和基差中枢回归等周期后，对于基差走势的判断更依赖于中长期的基本面视角。同时由于套保方在持仓量较大的情况下需要考虑流动性的条件，移仓周期内可以选择的展期时间点并不多，另外通过把移仓分配到多个交易日也可以相对减少短期价差波动的风险。对冲比率的研究则更关注整个投资组合的波动率和对冲成本的控制。通过对金融期货的期现时间序列进行检验，我们发现国债期货由于现货标的的特殊性，其最廉可交割券的切换和持有成本的存在，使得期现走势并不符合协整性的要求。然而即便是对于股指这样期现相对应的品种，走势仍然存在背离的情形。因此如何合理的运用套保比率和展期方法来有效对冲风险并减少成本是每个经济周期内都值得考量的问题。

　　套期保值的比率决定了投资组合整体风险暴露的程度，净多空仓位都会影响组合波动和收益表现。由于期现的联动反映一直是在不断变化的，静态套期保值的结果包含有偏估计，动态套期保值也逐渐成为研究的重点。理论上自回归条件异方差模型（ARCH）解决了数据异方差问题对于套期保值比率的影响，而广义自回归条件异方差模型（GARCH）又在此基础上有所改进。本文以沪深300、中证500和上证50股指期货进行实证分析，中证1000合约由于数据较少没有被纳入测算。通过OLS、VAR、ECM和GARCH模型计算出套期保值比例；根据现货市场、期货市场以及套保比例，评估净值曲线，同时选取多个指标评估净值曲线的表现，进而找到不同品种的最优模型。

　　从三大股指合约的套保效果来看，OLS方法在IF和IC上表现较差，与基准策略基本持平，而在IH上测试显示相对更好。其他三个统计模型均要优于基准策略，且计算的数值相对也比较接近，这与回归多项式的原理有一定关系。对于IH合约而言，VAR模型相对更优；对于IC合约，三个方法差异并不显著，GARCH方法相对更好。

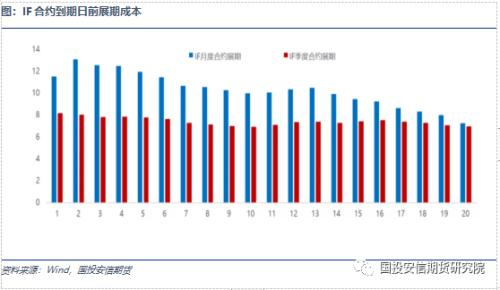
　　此外，本文还将测试展期日对组合净值表现的影响，选取当月合约到期日前1-15天作为移仓日，观察净值变化情况，选择较优的移仓日。套期保值比率调整的周期也是动态套期保值中重要的一环，周期的调整会结合市场实际的情况进行多个周期的检验，进而寻找较为适宜的调整频率。我们先假设套保比例为1，选择股指期货合约到期前1-15天。从移仓单日最大亏损、移仓累计收益和年化收益率等进行评价，对回测区间的期指合约的移仓日期进行设置。

　　统计模型-套保比率

　　套期保值比例可以通过统计回归模型得到。常用的统计模型有OLS、VAR、ECM和M-GARCH模型。本文通过OLS、VAR、ECM和GARCH模型求出套保比例进行比较。

　　2.1OLS回归模型

　　OLS是最为基础的统计回归模型。OLS模型的前提假设条件为误差序列同方差且无相关性，即：

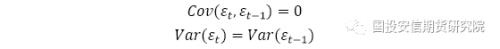
　　当上述条件不满足时，模型回归的结果是有偏的。

　　现货收益和期货收益的OLS回归模型如下式所示：

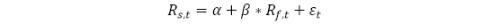
　　其中，Rs，t为t时间现货的收益，Rf，t为t时间期货的收益。

　　在该模型中，回归系数β即为套保比例。

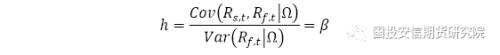
　　2.2VAR模型

　　对于经济变量来说，序列往往存在自相关性。向量自回归模型的提出解决了序列自相关问题。现货收益和期货收益的VAR模型如下式所示：

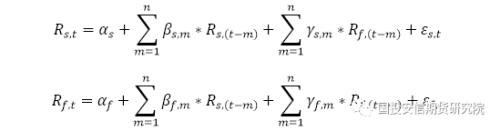
　　其中，εs，t和εf，t分别为现货收益和期货收益回归的误差序列，各项均服从正态分布；n为自回归滞后阶数。在VAR模型中，套期保值比例为：

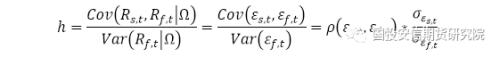
　　根据VAR模型回归结果的AIC值变化，我们设置最大滞后阶数为3。

　　2.3ECM模型

　　对于非平稳的序列来说，OLS和VAR模型不再适用。为解释存在协整关系的序列，即变量之间存在长期均衡的关系，我们在VAR模型的基础上引入误差修正项，建立ECM模型：

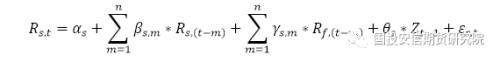
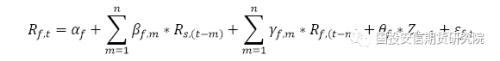
　　其中：

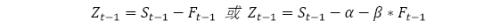
　　St-1为现货在t-1时刻的价格，Ft-1为期货在t-1时刻的价格。

　　该模型得到的套期保值比例为：

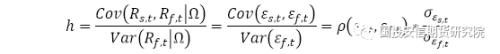
　　2.4GARCH模型

　　针对残差项，上述三个模型均假设残差项为同方差，但大量的实证研究表明，金融时间序列存在残差项异方差的问题，因此GARCH模型被提出。具体模型如下：

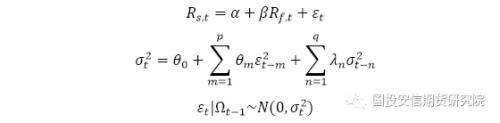
　　最优套期保值比例为：

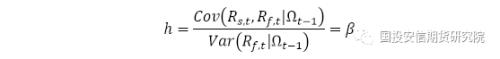
　　我们选取2016年1月至2022年7月的历史数据作为研究对象，用合约到期前1年的交易数据（252天）来确定套保比例。在选取合约到期前10天作为股指期货移仓日，并且期货合约杠杆为1的条件下，所选取的股指期货在OLS、VAR、ECM和GARCH模型下套期保值组合的净值表现如附表所示。

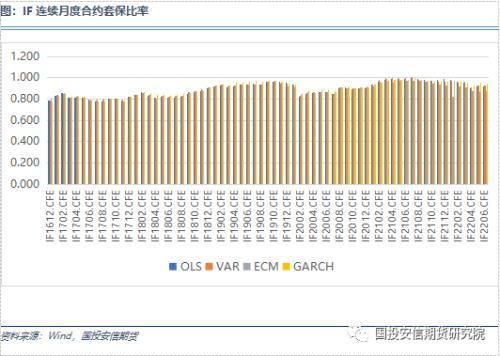
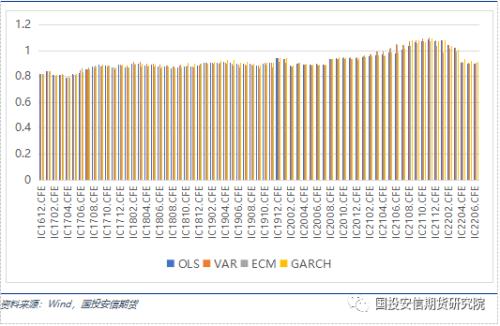
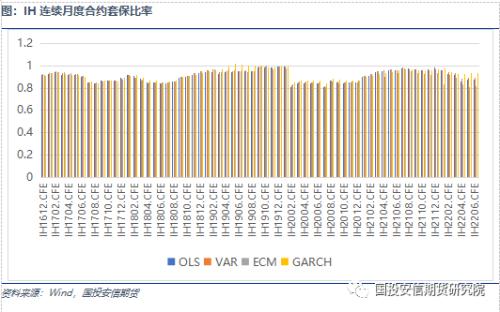
　　接下来，我们通过以下五个指标来评估套保组合的净值表现：移仓单日最大亏损、移仓累计收益、年化收益率、最大回撤率和夏普率。对于标的沪深300、中证500和上证50股指期货，在四个模型下的套保组合的净值表现分别与基准策略，即市值对冲方法进行比较。

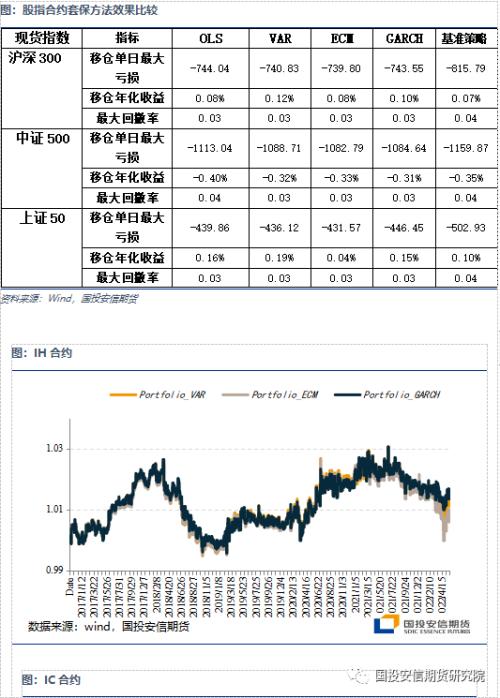
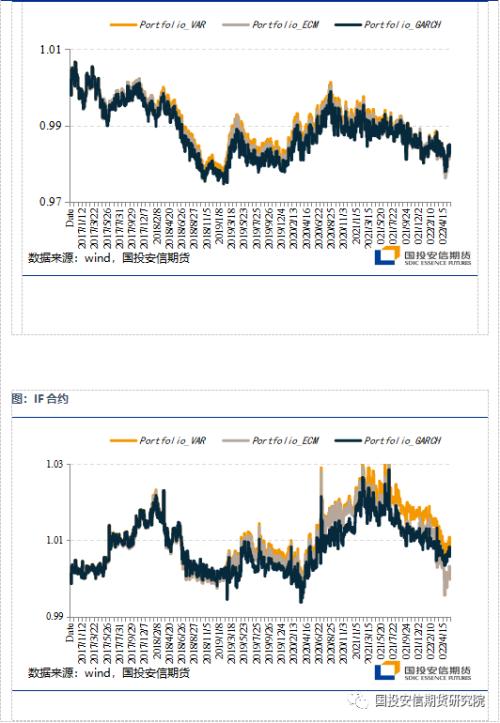
　　通过对不同套期保值方法的比较，统计模型计算的套保比率在不断上升，头寸敞口也在不断缩小，这与近年来期指市场的参与结构的完善，贴水中枢的收敛都有一定关联。从三大股指合约的套保效果来看，OLS方法在IF和IC上表现较差，与基准策略基本持平，在IH上测试显示相对更好。其他三个统计模型均要优于基准策略，且计算的数值相对也比较接近，这与回归多项式的原理有一定关系。对于IH合约而言，VAR模型相对更优；对于IC合约，三个方法差异并不显著，GARCH方法相对更好。由于套保比率原本就是在风险敞口方面的调整，对于整体投资组合收益率的改变并不显著，但是对于波动率的降低仍然有一定作用，尤其是在面临不利的移仓区间内，合理套保头寸能够降低7％的当期对冲成本。